题目内容
16.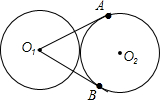 如图,两个等圆⊙O1和⊙O2外切,过点O1作⊙O2的两条切线OA、OB,A、B为切点,则∠AO1B=60°.
如图,两个等圆⊙O1和⊙O2外切,过点O1作⊙O2的两条切线OA、OB,A、B为切点,则∠AO1B=60°.
分析 根据切线的性质以及相切两圆的性质得出O1A⊥O2A,2AO2=O2O1,∠AO1B=2∠AO1O2,进而求出∠AO1B度数.
解答 解:连接AO2,O2O1,BO2,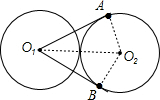
∵两个等圆⊙O2和⊙O1相切,过点O1作圆O2的两条切线O1A、O1B,切点为A、B,
∴O1A⊥O2A,2AO2=O2O1,∠AO1B=2∠AO1O2,
∴∠AO1O2=30°,
∴∠AO1B=60°.
故答案为:60°.
点评 此题主要考查了相切两圆的性质以及切线的性质,根据已知得出∠AO1O2的度数是解题关键.

练习册系列答案
相关题目
11.下列命题中,真命题的是( )
| A. | 两个锐角的和为直角 | B. | 两个锐角的和为钝角 | ||
| C. | 两个锐角的和为锐角 | D. | 互余且非零度的两个角都是锐角 |
1.函数y=$\sqrt{4-x}$中,自变量x的取值范围( )
| A. | x>4 | B. | x<4 | C. | x≥4 | D. | x≤4 |
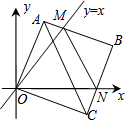 在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.
在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.