题目内容
10. 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )| A. | -1≤b≤$\frac{1}{2}$ | B. | -1≤b≤1 | C. | -$\frac{1}{2}$≤b≤1 | D. | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
分析 将A(-3,1),B(-1,1),C(-2,2)的坐标分别代入直线y﹦-$\frac{1}{2}$x+b中求得b的值,再根据一次函数的增减性即可得到b的取值范围.
解答 解:将A(-3,1)代入直线y﹦-$\frac{1}{2}$x+b中,可得$\frac{3}{2}$+b=1,解得b=-$\frac{1}{2}$;
将B(-1,1)代入直线y﹦-$\frac{1}{2}$x+b中,可得$\frac{1}{2}$+b=1,解得b=$\frac{1}{2}$;
将C(-2,2)代入直线y﹦-$\frac{1}{2}$x+b中,可得1+b=2,解得b=1.
故b的取值范围是-$\frac{1}{2}$≤b≤1.
故选C.
点评 考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.

练习册系列答案
相关题目
1.函数y=$\sqrt{4-x}$中,自变量x的取值范围( )
| A. | x>4 | B. | x<4 | C. | x≥4 | D. | x≤4 |
 如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.
如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.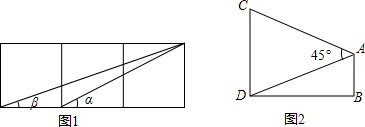
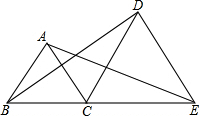 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.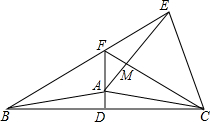 已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.  如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,其中A(1,-3),B(3,-4),C(4,-1);
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,其中A(1,-3),B(3,-4),C(4,-1);