题目内容
12．
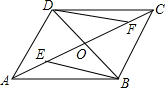如图，在平行四边形ABCD中，AC，BD相交于点O，点E，F在AC上，且OE=OF．（1）求证：BE=DF；
（2）线段OE满足什么条件时，四边形BEDF为矩形（不必证明）．
分析 （1）连接BE、DF，根据平行四边形的性质可得DO=BO，再由OE=OF可得四边形DEBF是平行四边形，进而可得DF=BE；
（2）当OE=DO时，可得EF=BD，根据对角线相等的平行四边形是矩形可得四边形BEDF为矩形．
解答 
（1）证明：连接BE、DF，
∵四边形ABCD是平行四边形，
∴DO=BO，
∵OE=OF，
∴四边形DEBF是平行四边形，
∴DF=BE；
（2）解：当OE=DO时，四边形BEDF为矩形．
点评 此题主要考查了平行四边形的判定和性质，以及矩形的判定，关键是掌握平行四边形的对角线互相平分；对角线互相平分的四边形是平行四边形．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
7．已知ab＜0，则$\sqrt{{a}^{2}b}$化简后为（ ）
| A． | a$\sqrt{b}$ | B． | -a$\sqrt{b}$ | C． | a$\sqrt{-b}$ | D． | -a$\sqrt{-b}$ |
