题目内容

1．如果一个二次函数的二次项系数为1，那么这个函数可以表示为y=x2+px+q，我们将p，q称为这个函数的特征数．例如二次函数y=x2-4x+2的特征数是-4，2．请根据以上的信息探究下面的问题：如果一个二次函数的特征数是2，3，将这个函数的图象先向左平移2个单位，再向下平移3个单位，那么此时得到的图象所对应的函数的特征数为6，8．

分析 首先得出函数解析式，进而利用函数平移规律得出答案．

解答 解：特征数是2，3的函数解析式为：y=x2+2x+3=（x+1）2+2，其顶点坐标是（-1，2），
将这个函数的图象先向左平移2个单位，再向下平移3个单位后的顶点坐标是（-3，-1），
所以平移后的函数解析式为：y=（x+3）2-1=x2+6x+8，那么此时得到的图象所对应的函数的特征数为 6，8．
故答案是：6，8．

点评 主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．会利用方程求抛物线与坐标轴的交点．

练习册系列答案
相关题目
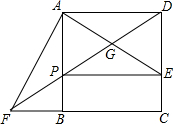11．如图，在正方形ABCD中，点E时CD边上一点，AF⊥AE交CB的延长线于点F，连接DF分别交于AE、AB于点C、P连接PE．
（1）求证：AE=AF；
（2）若AD=2，求当DE为何值时，四边形APED是矩形．
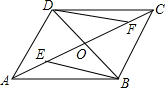12．如图，在平行四边形ABCD中，AC，BD相交于点O，点E，F在AC上，且OE=OF．
（1）求证：BE=DF；
（2）线段OE满足什么条件时，四边形BEDF为矩形（不必证明）．
9．阅读下列材料，并解决后面的问题．
材料：一般地，n个相同的因数a相乘：$\underset{\underbrace{a•a…a}}{n}$记为an．如23=8，此时，3叫做以2为底8的对数，记为log28（log28=3）．一般地，若an=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为logab（即logab=n）．如34=81，则4叫做以3为底81的对数，记为log381（即log381=4）．则log24，log216，log264之间满足的关系式log24+log216=log264．
16．已知关于x的一元二次方程x2-6x+m-1=0有两个相等的实数根，那么m的值为10．
6．已知a，b两数在数轴上对应的点如图所示，下列结论中正确的是（　　）
A．a＜bB．ab＜0C．b-a＞0D．a+b＜0
13．我区积极开展“体育大课间”活动，引导学生坚持体育锻炼．某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：足球四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题：
（1）求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数；
（2）请把条形统计图补充完整；
（3）已知该校有1000人，请根据样本估计全校最喜欢足球的人数是多少？
10．春节过后，6名村民用1200元共同租用一辆小客车去广东工作．出发时又增加部分村民，结果每位村民比原来少分摊50元．求增加村民的人数．
11．已知抛物线y=ax2-2ax-4与x轴交于点A、B（A左B右），与 y轴交于点C，△ABC的面积为12．
（1）求抛物线的表达式；
（2）若点P在x轴上方的抛物线上，且tan∠PAB=$\frac{1}{2}$，求点P的坐标；
（3）在（2）的条件下，过C作射线交线段AP于点E，使得tan∠BCE=$\frac{1}{2}$，连结BE，求证：BE⊥BC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网