题目内容
2.某商店如果将进货价为8元的商品按每件10元出售,每天可销售200件.现采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件.问应将售价定为多少时,才能使每天所赚利润达到720元?分析 售价为x元,则有(x-进价)(每天售出的数量-$\frac{x-10}{0.5}$×10)=每天利润,解方程求解即可.
解答 解:设售价为x元,根据题意列方程得(x-8)(200-$\frac{x-10}{0.5}$×10)=720,
整理得:(x-8)(400-20x)=720,即x2-28x+192=0,
解得x1=12,x2=14.
故将每件售价定为12或14元时,才能使每天利润为720元.
又题意要求采取提高商品售价减少销售量的办法增加利润,
故应将商品的售价定为14元.
点评 本题考查的是一元二次方程的应用.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
7.已知-2<m<3,化简$\sqrt{(m-3)^{2}}$+|m+2|的结果是( )
| A. | 5 | B. | 1 | C. | 2m-1 | D. | 2m-5 |
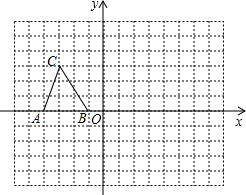 如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).
如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).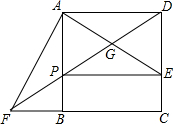 如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.
如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.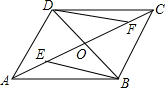 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.