题目内容
4.在某两个时刻,太阳光线与地面的夹角分别为37°和45°,树AB长6m.(1)如图①,若树与地面l的夹角为90°,则两次影长的和CD=14m;
(2)如图②,若树与地面l的夹角为α,求两次影长的和CD(用含α 的式子表示).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
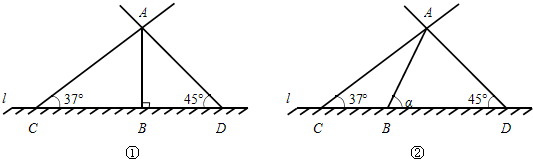
分析 (1)在RT△ABC中,依据正切函数求得BC的长,在△ABD中根据等角对等边求得BD的长,进而就可求得CD的长.
(2)作AE⊥地面于E,在RT△ABE中,依据正弦函数求得AE的长,在RT△AEC中,依据正切函数求得EC的长,在△AED中根据等角对等边求得ED的长,进而就可求得CD的长.
解答 解;(1)在RT△ABC中,∵∠C=37°,
∴BC=$\frac{AB}{tan37°}$=$\frac{6}{0.75}$≈8,
在RT△ABD中,∵∠ADB=45°,
∴∠DAB=∠ADB=45°,
∴BD=AB=6,
∴CD=BC+BD=8+6=14(m);
故答案为14;
(2)作AE⊥地面于E,
在RT△ABE中,∵∠ABE=α,
∴AE=AB•sinα=6•sinα,
在RT△ACE中,∵∠C=37°,
∴CE=$\frac{AE}{tan37°}$=$\frac{6•sinα}{0.75}$≈8•sinα,
在RT△AED中,∵∠ADB=45°,
∴∠DAB=∠ADB=45°,
∴ED=AE=6•sinα,
∴CD=EC+ED=8•sinα+6•sinα=14•sinα(m);
点评 本题考查了学生利用三角函数解决实际问题的能力以及等腰三角形的性质.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.

练习册系列答案
相关题目
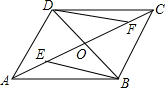 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF. 将矩形ABCD(如图)绕点A旋转后,点D落在对角线AC上的点D′,点C落到C′,如果AB=3,BC=4,那么CC′的长为$\sqrt{10}$.
将矩形ABCD(如图)绕点A旋转后,点D落在对角线AC上的点D′,点C落到C′,如果AB=3,BC=4,那么CC′的长为$\sqrt{10}$.