题目内容
17.我们定义:平面内两条直线l1、l2相交于点O(l1与l2不垂直),对于该平面内任意一点P,如果点P到直线l1、l2的距离分别为a、b,那么有序实数对(a,b)就叫做点P的“平面斜角坐标”.如果常数m、n都是正数,那么在平面内与“平面斜角坐标”(m,n) 对应的点共有4个.
分析 根据两条相交直线把平面分成四部分,在每一个部分内都存在一个满足要求距离的坐标解答.
解答 解:如图,
直线l1,l2把平面分成四个部分,
在每一部分内都有一个“距离坐标”为(m,n)的点,
所以,共有4个.
故答案为:4.
点评 本题考查了点到直线的距离,点的坐标的类比利用,读懂题目信息并且理解两条相交直线把平面分成四部分是解题的关键.

练习册系列答案
相关题目
7.已知-2<m<3,化简$\sqrt{(m-3)^{2}}$+|m+2|的结果是( )
| A. | 5 | B. | 1 | C. | 2m-1 | D. | 2m-5 |
8.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 5,12,14 | B. | 6,8,10 | C. | 7,24,25 | D. | 8,15,17 |
5.下列各式中计算正确的是( )
| A. | $\sqrt{(-1)(-9)}$=$\sqrt{-1}$•$\sqrt{-9}$=(-1)(-3)=3 | B. | $\sqrt{(-2)^{2}}$=-2 | ||
| C. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | D. | $\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7 |
2. 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )| A. | 30° | B. | 45° | C. | 120° | D. | 90° |
6. 已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
 已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )| A. | a<b | B. | ab<0 | C. | b-a>0 | D. | a+b<0 |
7.如果(x-2)(x+3)=x2+px+q,那么p、q的值为( )
| A. | p=5,q=6 | B. | p=1,q=-6 | C. | p=1,q=6 | D. | p=5,q=-6 |
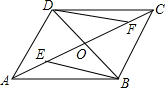 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.