题目内容
20.已知等腰△ABC的两条边长分别为4cm和6cm,则等腰△ABC的内切圆半径为$\sqrt{2}$或$\frac{3\sqrt{7}}{7}$cm.分析 如图,设三角形的内切圆为⊙O,切点分别为D、E、F,连接AO、BO,过AD⊥BC与D,由于△ABC是等腰三角形,由此可以确定A、O、D三点在同一直线上,可以利用勾股定理求出AD的长度,首先根据切线长定理求出AE,设OE=r,根据已知条件可以得到△ADB∽△AEO,最后利用相似三角形的性质即可求解.
解答 解:如图,设三角形的内切圆为⊙O,切点分别为D、E、F, 过AD⊥BC与D,
过AD⊥BC与D,
设OE=OD=OF=rcm,
∵△ABC是等腰三角形,
∴可以确定A、O、D三点在同一直线上,D是BC的中点,
当BC=4时,AB=AC=6,
∴BD=2cm,而AB=6cm,
∴AD=$\sqrt{{AB}^{2}{-BD}^{2}}$=$\sqrt{2}$,
根据切线长定理得AE=AF,BD=BE,CD=CF,
∴AE=AF=(AB+AC-BC)÷2=4,
∵AB是内切圆的切线,
∴∠AEO=90°=∠ADB,∠A=∠A,
∴△ADB∽△AEO,
∴OE:BD=AE:AD
设OE=r,
∴r:2=4:4$\sqrt{2}$,
∴r=$\sqrt{2}$cm.
当BC=6,则AB=AC=4,
∴BD=3,
∴AD=$\sqrt{{AB}^{2}{-BD}^{2}}$=$\sqrt{7}$,
根据切线长定理得AE=AF,BD=BE,CD=CF,
∴AE=AF=(AB+AC-BC)÷2=1,
∵AB是内切圆的切线,
∴∠AEO=90°=∠ADB,∠A=∠A,
∴△ADB∽△AEO,
∴OE:BD=AE:AD
设OE=r,
∴r:3=1:$\sqrt{7}$,
∴r=$\frac{3\sqrt{7}}{7}$cm.
故答案为:$\sqrt{2}$或$\frac{3\sqrt{7}}{7}$.
点评 本题考查了三角形的内切圆与内心的性质,也利用了等腰三角形的性质和勾股定理,有一定的综合性,能力要求比较高.

| A. | 5,12,14 | B. | 6,8,10 | C. | 7,24,25 | D. | 8,15,17 |
| A. | $\sqrt{(-1)(-9)}$=$\sqrt{-1}$•$\sqrt{-9}$=(-1)(-3)=3 | B. | $\sqrt{(-2)^{2}}$=-2 | ||
| C. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | D. | $\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7 |
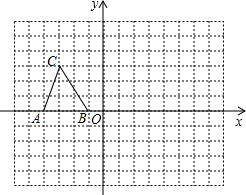 如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).
如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).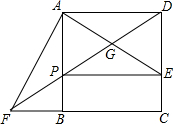 如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.
如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.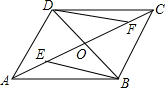 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.