题目内容
13.已知2+$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |
分析 首先设方程x2-4x+c=0的另一根为α,由根与系数的关系即可求得另一个根与c的值.
解答 解:设方程x2-4x+c=0的另一根为α,
则α+2+$\sqrt{3}$=4,
解得α=2-$\sqrt{3}$.
所以c=(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1.
故选:A.
点评 本题考查了根与系数的关系.若二次项系数为1,常用以下关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q,反过来可得p=-(x1+x2),q=x1x2,前者是已知系数确定根的相关问题,后者是已知两根确定方程中未知系数.

练习册系列答案
相关题目
4. 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )| A. | 17° | B. | 34° | C. | 56° | D. | 68° |
 如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度.
如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度. 某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.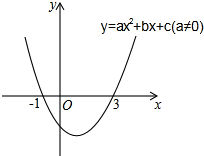 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )