题目内容
1. 某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.(1)如果各种选购方案被选中的可能性相同,那么利用树状图或列表方法求出A型号计算器被选中的概率是多少?
(2)现知新华中学购买甲、乙两种品牌计算器共40个(价格如图所示),恰好用了1000元人民币,其中甲品牌计算器为A型号计算器,求购买的A型号计算器有多少个?
分析 (1)利用树状图展示所有6种等可能的结果数,再找出选中A型号计算器的结果数,然后根据概率公式求解;
(2)讨论:当选用方案(A,D)时,设购买A型号,D型号计算器分别为x,y个,根据题意得$\left\{\begin{array}{l}{x+y=40}\\{60x+50y=1000}\end{array}\right.$,;当选用方案(A,E)时,设购买A型号、E型号计算器分别为m,n个,根据题意得$\left\{\begin{array}{l}{m+n=40}\\{60m+20n=1000}\end{array}\right.$,然后分别解方程组即可得到答案.
解答 解:(1)画树状图为: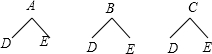
共有6种等可能的结果数,其中选中A型号计算器的结果数为2,
所以A型号计算器被选中的概率=$\frac{2}{6}$=$\frac{1}{3}$;
(2)由(2)可知,当选用方案(A,D)时,设购买A型号,D型号计算器分别为x,y个,根据题意得$\left\{\begin{array}{l}{x+y=40}\\{60x+50y=1000}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-100}\\{y=140}\end{array}\right.$,经检验不符合题意,舍去;
当选用方案(A,E)时,设购买A型号、E型号计算器分别为m,n个,根据题意得$\left\{\begin{array}{l}{m+n=40}\\{60m+20n=1000}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=5}\\{n=35}\end{array}\right.$,
所以新华中学购买了5个A型号计算器.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了二元一次方程组的应用.

 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
| A. | 3 | B. | ±6 | C. | 6 | D. | ±3 |
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |

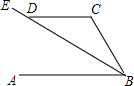 如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.
如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.