题目内容
8.关于x的分式方程$\frac{1-m}{2-x}=\frac{1}{2}$的解为正数,则m的取值范围是m>0且m≠1.分析 根据解分式方程的一般步骤,可得分式方程的解,根据解为正数,可得不等式,解不等式即可得答案.
解答 解:∵关于x的分式方程$\frac{1-m}{2-x}=\frac{1}{2}$的解为正数,
∴x=2m>0且2m≠2,
∴m>0且m≠1;
故答案为:m>0且m≠1;
点评 此题主要考查了分式方程的解,解出分式方程,根据解为正数列出不等式是解题关键.

练习册系列答案
相关题目
19.正比例函数y=2x的图象与反比例函数y=$\frac{2}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
3.用科学记数法表示0.0000907,得( )
| A. | 9.07×10-4 | B. | 9.07×10-6 | C. | 9.07×105 | D. | 9.07×10-5 |
13.已知2+$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |
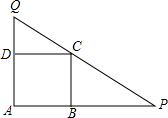 如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值. 如图中的两条直线l1,l2可以看作方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=-x+4}\end{array}\right.$的解.
如图中的两条直线l1,l2可以看作方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=-x+4}\end{array}\right.$的解.