题目内容
4. 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )| A. | 17° | B. | 34° | C. | 56° | D. | 68° |
分析 首先由AB∥CD,求得∠ABC的度数,又由BC平分∠ABE,求得∠CBE的度数,然后根据三角形外角的性质求得∠BED的度数.
解答 解:∵AB∥CD,
∴∠ABC=∠C=34°,
∵BC平分∠ABE,
∴∠CBE=∠ABC=34°,
∴∠BED=∠C+∠CBE=68°.
故选D.
点评 此题考查了平行线的性质,角平分线的定义以及三角形外角的性质.此题难度不大,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
14.2014年吉林省对全省供热管网进行改造,改造后全年二氧化碳排放量共减少7620000吨,7620000这个数用科学记数法表示为( )
| A. | 762×104 | B. | 76.2×105 | C. | 7.62×106 | D. | 0.762×107 |
19.正比例函数y=2x的图象与反比例函数y=$\frac{2}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
13.已知2+$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |


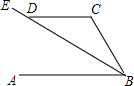 如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.
如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.