题目内容
5.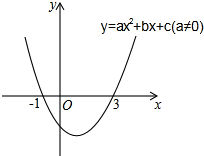 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )| A. | ①②④ | B. | ①③ | C. | ①②③ | D. | ①③④ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵函数图象的对称轴为:x=-$\frac{b}{2a}$=$\frac{-1+3}{2}$=1,
∴b=-2a,即2a+b=0,①正确;
由图象可知,当-1<x<3时,y<0,②错误;
由图象可知,当x=1时,y=0,
∴a-b+c=0,
∵b=-2a,
∴3a+c=0,③正确;
∵抛物线的对称轴为x=1,开口方向向上,
∴若(x1,y1)、(x2,y2)在函数图象上,当1<x1<x2时,y1<y2;当x1<x2<1时,y1>y2;
故④错误;
故选:B.
点评 本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数的性质,抛物线与x轴的交点,难度适中.

练习册系列答案
相关题目
13.已知2+$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |

 如图中的两条直线l1,l2可以看作方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=-x+4}\end{array}\right.$的解.
如图中的两条直线l1,l2可以看作方程组$\left\{\begin{array}{l}{y=2x+1}\\{y=-x+4}\end{array}\right.$的解.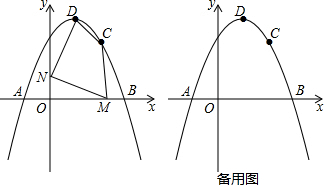
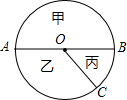 如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1
如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1