题目内容
3. 如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度.
如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度.
分析 延长FE交AC于点G,根据平行线的性质求出∠CGE的度数,再由三角形外角的性质即可得出结论.
解答 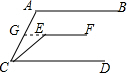 解:延长FE交AC于点G,
解:延长FE交AC于点G,
∵AB∥EF,∠A=115°,
∴∠CGE=∠A=115°.
∵∠E=140°,
∴∠ACE=∠CEF-∠CGE=140°-115°=25°.
故答案为:25.
点评 本题考查的是平行线的性质,根据题意作出辅助线,利用三角形外角的性质求解是解答此题的关键.

练习册系列答案
相关题目
14.2014年吉林省对全省供热管网进行改造,改造后全年二氧化碳排放量共减少7620000吨,7620000这个数用科学记数法表示为( )
| A. | 762×104 | B. | 76.2×105 | C. | 7.62×106 | D. | 0.762×107 |
11. 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
8.在数轴上任取一个比-5大比7小的实数a对应的点,则取到的点对应的实数a满足|a|>2的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{6}{11}$ | D. | $\frac{2}{3}$ |
13.已知2+$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |
 AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数为151°.
AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数为151°.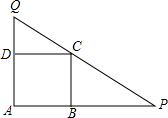 如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
