题目内容
2．已知x1，x2是方程x2-$\sqrt{5}$x+1=0的两根，则x12+x22的值为（ ）| A． | -$\frac{3}{4}$ | B． | 3 | C． | 7 | D． | $\sqrt{5}$ |
分析 根据根与系数的关系即可得出x1+x2=$\sqrt{5}$、x1•x2=1，将x12+x22变形为$（{x}_{1}+{x}_{2}）^{2}$-2x1•x2，代入数据即可得出结论．
解答 解：∵x1，x2是方程x2-$\sqrt{5}$x+1=0的两根，
∴x1+x2=$\sqrt{5}$，x1•x2=1，
∴x12+x22=$（{x}_{1}+{x}_{2}）^{2}$-2x1•x2=3．
故选B．
点评 本题考查了根与系数的关系，熟练掌握x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$是解题的关键．
练习册系列答案
相关题目
已知y与x-3成正比例，当x=4时，y=3．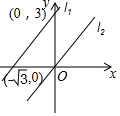
如图，直线L1过点（0，3），（-$\sqrt{3}$，0）．
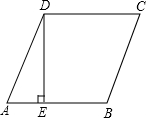如图所示，在菱形ABCD中，DE⊥AB于E，BE=16cm，sinA=$\frac{12}{13}$，求此菱形的周长．