题目内容
13.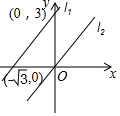 如图,直线L1过点(0,3),(-$\sqrt{3}$,0).
如图,直线L1过点(0,3),(-$\sqrt{3}$,0).(1)求直线L1的函数表达式;.
(2)直线L2过原点O,且与直线L1平行,求L1与L2之间的距离;
(3)点M(a,b)是第一象限且位于直线L1下方的任意一点.求点M到直线L1的距离.
分析 (1)设直线L1的函数表达式为y=kx+b,由直线L1过点(0,3),(-$\sqrt{3}$,0).列方程组即可得到结论;
(2)根据三角函数的定义即可得到结论;
(3)根据点到直线的距离公式即可得到结论.
解答 解:(1)设直线L1的函数表达式为y=kx+b,
∵直线L1过点(0,3),(-$\sqrt{3}$,0).
∴$\left\{\begin{array}{l}{-\sqrt{3}k+b=0}\\{b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=3}\end{array}\right.$,
∴直线L1的函数表达式为:y=$\sqrt{3}$x+3;
(2)∵直线L2过原点O,且与直线L1平行,
∴L1与L2之间的距离=$\frac{3}{2}$;
(3)点M到直线L1的距离=$\frac{|\sqrt{3}a-b+3|}{2}$,
∵点M(a,b)是第一象限且位于直线L1下方的任意一点.
∴点M到直线L1的距离=$\frac{\sqrt{3}a-b+3}{2}$.
点评 本题考查了两直线橡胶或平行,点到直线的距离公式,平行线间的距离的计算,正确的理解题意是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
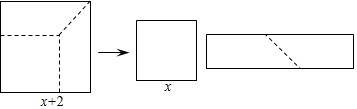
5.如图,边长为x+2的正方形纸片剪出一个边长为x的正方形后,剩余部分可剪拼成一个长方形,则拼成的长方形的面积为( )

| A. | 2x+2 | B. | 4x+4 | C. | x+4 | D. | 2x-2 |
2.已知x1,x2是方程x2-$\sqrt{5}$x+1=0的两根,则x12+x22的值为( )
| A. | -$\frac{3}{4}$ | B. | 3 | C. | 7 | D. | $\sqrt{5}$ |
3.解方程2x+3(2x-1)=16-(x+1)的第一步应是( )
| A. | 去分母 | B. | 去括号 | C. | 移项 | D. | 合并 |
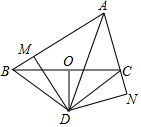 如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
 如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.
如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.