题目内容
12. 已知y与x-3成正比例,当x=4时,y=3.
已知y与x-3成正比例,当x=4时,y=3.(1)求出y与x之间的函数关系式;
(2)y与x之间是什么函数关系?并在平面直角坐标系中画出该函数的图象;
(3)当x=2.5时,y的值为-1.5.
分析 (1)根据y与x-3成正比例,设出一次函数的关系式,再把当x=4时,y=3代入求出k的值即可;
(2)根据一次函数的定义可得y与x之间的函数关系,再根据描点法画出函数即可求解;
(3)根据代入法即可求解.
解答 解:(1)∵y与x-3成正比例,设出一次函数的关系式为:y=k(x-3)(k≠0),
把当x=4时,y=-3代入得:3=(4-3)k,解得k=3,
∴y与x之间的函数关系式为:y=3(x-3)=3x-9.
(2)y是x的一次函数,该函数的图象如图所示;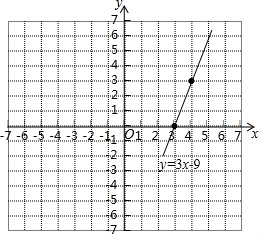
(3)当x=2.5时,y=3×2.5-9=-1.5.
故答案为:-1.5.
点评 本题考查的是用待定系数法求一次函数的解析式,此类方法是求函数解析式常用的方法.

练习册系列答案
相关题目
17.为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9-6)=24(元)
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
| 用水量 | 单价 |
| 不超过6m3的部分 | 2元/m3 |
| 超过6m3不超过10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
2.已知x1,x2是方程x2-$\sqrt{5}$x+1=0的两根,则x12+x22的值为( )
| A. | -$\frac{3}{4}$ | B. | 3 | C. | 7 | D. | $\sqrt{5}$ |
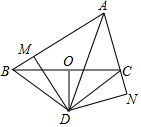 如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.