题目内容
10.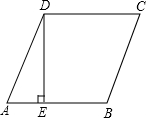 如图所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周长.
如图所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周长.
分析 由DE⊥AB,sinA=$\frac{DE}{AD}$=$\frac{12}{13}$,设DE=12k,AD=13k,则AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{(13k)^{2}-(12k)^{2}}$=5k,根据EB=13k-5k=8k=16,得到k=2,AD=26,由此即可解决问题.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵DE⊥AB,sinA=$\frac{DE}{AD}$=$\frac{12}{13}$,设DE=12k,AD=13k,
则AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{(13k)^{2}-(12k)^{2}}$=5k,
∴EB=13k-5k=8k=16,
∴k=2,AD=26,
∴菱形的周长为104cm
点评 本题考查菱形的性质、锐角三角函数、勾股定理等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
5.如图,边长为x+2的正方形纸片剪出一个边长为x的正方形后,剩余部分可剪拼成一个长方形,则拼成的长方形的面积为( )
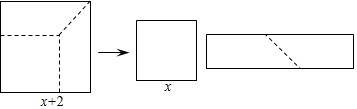

| A. | 2x+2 | B. | 4x+4 | C. | x+4 | D. | 2x-2 |
2.已知x1,x2是方程x2-$\sqrt{5}$x+1=0的两根,则x12+x22的值为( )
| A. | -$\frac{3}{4}$ | B. | 3 | C. | 7 | D. | $\sqrt{5}$ |
19.下列汽车标志中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.
如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.