题目内容
20. 如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.(1)求一次函数与反比例函数的解析式.
(2)当x为何值时,y1<y2?
分析 (1)由反比例函数图象上点坐标的特点可求出k值的大小,从而得出反比例函数解析式;由三角形的面积公式可得出AB=4,结合点B坐标可得出点A的坐标,由A、P点的坐标利用待定系数法即可求出一次函数的解析式;
(2)令y1=y2,求出x的值,从而得出点Q的横坐标,结合两函数图象的位置关系即可得出结论.
解答 解:(1)∵点P的坐标为(2,2),
∴k=2×2=4,
∴反比例函数解析式为y2=$\frac{4}{x}$.
∵S△ABC=$\frac{1}{2}$AB•PB=4,
∴AB=4,
∴点A(-2,0).
∵点A、P在一次函数图象上,
∴有$\left\{\begin{array}{l}{0=-2m+n}\\{2=2m+n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=1}\end{array}\right.$.
∴一次函数解析式为y1=$\frac{1}{2}$x+1.
(2)令y1=$\frac{1}{2}$x+1=y2=$\frac{4}{x}$,即x2+2x-8=0,
解得:x1=-4,x2=2.
即点Q横坐标为-4,点P横坐标为2.
结合两函数图象可知:
当x<-4和0<x<2时,一次函数图象在反比例函数图象下方,
则当x<-4或0<x<2时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、三角形的面积公式以及待定系数法求函数解析式,解题的关键是:(1)求出点A的坐标;(2)结合函数图象的位置关系解不等式.本题属于基础题,难度不大,解决该题型题目时,根据给定的条件求出点的坐标,再根据点的坐标利用待定系数法求函数解析式是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.已知直线y=kx+b过点A(x1,y1),点B(x2,y2),若x1<x2时,有y1>y2,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | k=0 | D. | 不能确定 |
15.给出下列函数:①y=2x;②y=-2x+1;③y=$\frac{2}{x}$(x>0);④y=x2(x<1),其中y随x的增大而减小的函数是( )
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ②③ |
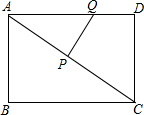 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.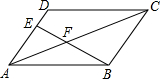 如图,在?ABCD中,点E在AD边上,AE=2ED,连接EB交AC于点F,若AC=10,则AF为4.
如图,在?ABCD中,点E在AD边上,AE=2ED,连接EB交AC于点F,若AC=10,则AF为4.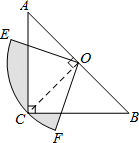 如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.
如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.