题目内容
12.已知函数y=x2+3kx+k+1的图象的顶点在y轴上,那么函数的关系式是y=x2+1.分析 由抛物线顶点在y轴上可知其对称轴是直线x=0,得关于k的方程,解方程可得k的值,代入可得.
解答 解:∵函数y=x2+3kx+k+1的图象的顶点在y轴上,
∴抛物线的对称轴是x=0,即-$\frac{3k}{2}$=0,
解得:k=0,
∴函数关系式为:y=x2+1,
故答案为:y=x2+1.
点评 本题主要考查二次函数的图象与性质,解题的关键是理解题意正确记忆顶点坐标公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.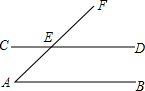 如图,直线AB∥CD,AF交CD于点E,∠CEA=45°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEA=45°,则∠A等于( )
 如图,直线AB∥CD,AF交CD于点E,∠CEA=45°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEA=45°,则∠A等于( )| A. | 35° | B. | 45° | C. | 50° | D. | 135° |
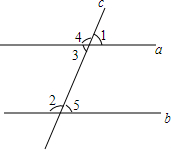 如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b.
如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b. 设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2).
设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2). 如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4. 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义: