题目内容
11.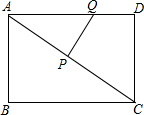 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△APQ与△ADC相似,求t的值.
(2)连结CQ,DP,若CQ⊥DP,求t的值.
(3)连结BQ,PD,请问BQ能和PD平行吗?若能,求出t的值;若不能,说明理由.
分析 (1)根据相似三角形的性质即可得到结论;
(2)过P作PM⊥AD于M,根据相似三角形的性质列比例式求得PM=3t,AM=4t,MD=8-4t,根据已知条件推出△PMD∽△QDC,根据相似三角形的性质列方程即可得到结论;
(3)设DP交BC于N,根据相似三角形的性质列比例式求得NC=$\frac{10-5t}{5t}×8=\frac{16-8t}{t}$,得到BN=8-$\frac{16-8t}{t}$=$\frac{16t-16}{t}$,当BQ∥DP,得到四边形BQDN是平行四边形,根据平行四边形的性质列方程即可得到结论.
解答 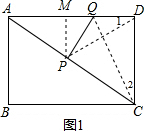 解:(1)由题意得;QD=4t,AQ=8-4t,AP=5t,PC=10-t,
解:(1)由题意得;QD=4t,AQ=8-4t,AP=5t,PC=10-t,
∵△APQ与△ADC相似,
∴情况①$\frac{AQ}{AC}=\frac{AP}{AD}$,即$\frac{8-4t}{10}=\frac{5t}{8}$,解得:t=$\frac{32}{41}$;
情况②$\frac{AQ}{AD}=\frac{AP}{AC}$,即$\frac{8-4t}{8}=\frac{5t}{10}$,解得:t=1;
(2)如图1,过P作PM⊥AD于M,∵∠ADC=90°,∴PM∥CD,∴△APM∽△ACD,
∴$\frac{PM}{CD}=\frac{AM}{AD}=\frac{AP}{AC}$,
∵AP=5t,
∴$\frac{PM}{6}=\frac{AM}{8}=\frac{5t}{10}$,
∴PM=3t,AM=4t,MD=8-4t,
∵CQ⊥DP,∴∠1=∠2,
∵∠PMD=∠CDQ=90°,
∴△PMD∽△QDC,
∴$\frac{PM}{QD}=\frac{MD}{DC}$,即$\frac{3t}{4t}=\frac{8-4t}{6}$,
解得:t=$\frac{7}{8}$;
(3)设DP交BC于N,
∵AD∥BC,
∴△ADP∽△CNP,
∴$\frac{NC}{AD}=\frac{CP}{AP}$,
∴NC=$\frac{10-5t}{5t}×8=\frac{16-8t}{t}$,
∴BN=8-$\frac{16-8t}{t}$=$\frac{16t-16}{t}$,
当BQ∥DP,则四边形BQDN是平行四边形,
∴BN=QD,
∴$\frac{16t-16}{t}$=4t,
解得:t1=t2=2,(不合题意,舍去),
∴不存在这样的t.
点评 本题考查了矩形的性质,相似三角形的判定和性质,垂直的定义,证得△ADP∽△CNP是解题的关键.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案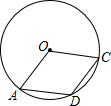 如图,在半径为6的⊙O中,D是$\widehat{AC}$上一点,∠ADC=115°,则$\widehat{AC}$的长为( )
如图,在半径为6的⊙O中,D是$\widehat{AC}$上一点,∠ADC=115°,则$\widehat{AC}$的长为( )| A. | $\frac{23}{6}$π | B. | $\frac{23}{3}$π | C. | $\frac{13}{3}$π | D. | $\frac{13}{6}$π |
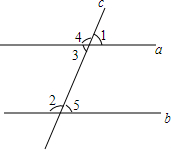 如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b.
如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b.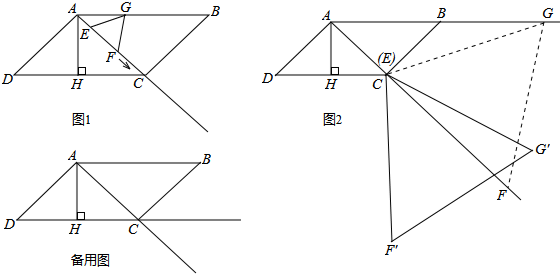
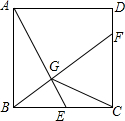 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.
如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1. 设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2).
设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2). 如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.