题目内容
9.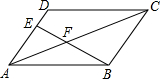 如图,在?ABCD中,点E在AD边上,AE=2ED,连接EB交AC于点F,若AC=10,则AF为4.
如图,在?ABCD中,点E在AD边上,AE=2ED,连接EB交AC于点F,若AC=10,则AF为4.
分析 根据平行四边形的对边相等可得AD=BC,然后求出AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,再根据平行线分线段成比例定理求出AF、FC的比,然后求解即可.
解答 解:在?ABCD中,AD=BC,AD∥BC,
∵AE=2ED,
∴AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,
∵AD∥BC,
∴$\frac{AF}{CF}=\frac{AE}{BC}$=$\frac{2}{3}$,
∵AC=10,
∴AF=$\frac{2}{2+3}$×10=4.
故答案为:4.
点评 本题考查了平行线分线段成比例定理,平行四边形的对边平行且相等的性质,熟记定理并求出AF、FC的比是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
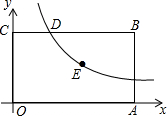 如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.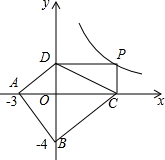 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )