题目内容
5.已知y-2与3x-4成正比例函数关系,且当x=2时,y=3.(1)写出y与x之间的函数解析式;
(2)若点P(a,-3)在这个函数的图象上,求a的值;
(3)若y的取值范围为-1≤y≤1,求x的取值范围.
分析 (1)根据正比例的定义设y-2=k(3x-4),然后把x=2时,y=3代入计算求出k值,再整理即可得解;
(2)将点(a,-3)代入(1)中所求的函数的解析式求a的值;
(3)分别代入y=-1和y=1,分别求出所对应的x的值,即可求得x的取值范围.
解答 解:(1)设y-2=k(3x-4),
将x=2、y=3代入,得:2k=1,解得k=$\frac{1}{2}$,
∴y-2=$\frac{1}{2}$(3x-4),即y=$\frac{3}{2}$x;
(2)将点P(a,-3)代入y=$\frac{3}{2}$x,得:$\frac{3}{2}$a=-3,
解得:a=-2;
(3)当y=-1时,$\frac{3}{2}$x=-1,解得:x=-$\frac{2}{3}$,
当y=1时,$\frac{3}{2}$x=1,解得:x=$\frac{2}{3}$,
故-$\frac{2}{3}$≤x≤$\frac{2}{3}$.
点评 本题综合考查了一次函数的性质、待定系数法求一次函数的解析式、一次函数图象上点的坐标特征.一次函数图象上的点的坐标都满足该函数的解析式.

练习册系列答案
相关题目
 如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
如图,一次函数y1=mx+n的图象分别交x轴、y轴于A、C两点,交反比例函数y2=$\frac{k}{x}$(k>0)的图象于P、Q两点.过点P作PB⊥x轴于点B,若点P的坐标为(2,2),△PAB的面积为4.
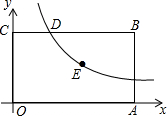 如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.