题目内容
14. 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB.(1)AE和DB有何大小关系,请说明理由;
(2)如果把△DCE绕点C顺时针再旋转一个角度,(1)中的结论还成立吗?
分析 (1)根据等边三角形边长相等的性质和各内角为60°的性质可求得△BCD≌△ACE,根据全等三角形对应边相等的性质即可求得AE=BD.
(2)根据题意画出图形,证明方法与(1)相同.
解答 解:(1)AE=DB,
∵△ABC、△DCE均为等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
∵在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD.
(2)成立,
成立AE=BD;理由如下:
如图,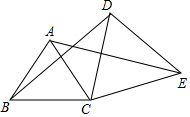
∵△ABC、△DCE均为等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
∵在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD.
点评 本题考查了等边三角形的性质的运用及全等三角形的判定和性质的运用.解决本题的关键是根据待求AE与BD明确所需求证的三角形全等.

练习册系列答案
相关题目
4.已知⊙O的半径R=$\sqrt{3}$cm,点O到直线l的距离为d,如果直线l与⊙O有公共点,那么( )
| A. | d≤$\sqrt{3}$cm | B. | d$<\sqrt{3}$cm | C. | d$≥\sqrt{3}$cm | D. | d$>\sqrt{3}$cm |
5.一组数据1,3,5,8,x的中位数是5,则下列x的取值中,满足条件的是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
2. 如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )
如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )
 如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )
如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )| A. | 1cm2 | B. | 2cm2 | C. | 0.25cm2 | D. | 0.5cm2 |
16.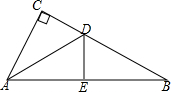 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
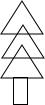 如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.
如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.