题目内容
9.一列数满足如下规律:第一个数a1=1,第二个数a2=-4,第三个数a3=7,第四个数a4=-10,…,则第n个数an可用含有n的代数式表示为(-1)n+1(3n-2).分析 由规律可知第一个数a1=1=(-1)1+1(3×1-2),第二个数a2=-4=(-1)2+1(3×2-2),第三个数a3=7=(-1)3+1(3×3-2),第四个数a4=-10=(-1)4+1(3×4-2),…,则第n个数为an=(-1)n+1(3n-2)
解答 解:∵由规律可知第一个数a1=1=(-1)1+1(3×1-2),
第二个数a2=-4=(-1)2+1(3×2-2),
第三个数a3=7=(-1)3+1(3×3-2),
第四个数a4=-10=(-1)4+1(3×4-2),
…,
则第n个数为an=(-1)n+1(3n-2)
故答案为:(-1)n+1(3n-2).
点评 本题主要考查了数字的变化规律,发现规律运用规律是解答此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.在平面直角坐标系中,已知点P的坐标是(3,4),点P与点Q关于y轴对称,则点Q的坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
10.小明用100元钱购得笔记本和笔共30件,已知每本笔记本2元,每支笔5元,那么小明最多能买笔的数目为
( )
( )
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
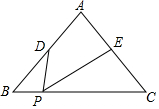 △ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4.
△ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4. 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB. 如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.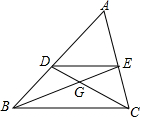 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.