题目内容
16.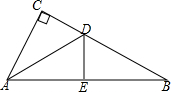 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
分析 利用HL得到直角三角形ACD与直角三角形AED全等,利用全等三角形对应角相等得到∠ADC=∠ADE,求出∠CDE的度数,即可求出∠BDE的度数.
解答 解:∵DE⊥AB,
∴∠C=∠AED=90°,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{AC=AE}\end{array}\right.$,
∴△ACD≌△AED(HL),
∴∠EDA=∠CDA=50°,
∴∠BDE=180°-∠ADC-∠EDA=80°,
故选D.
点评 本题考查了全等三角形的判定与性质、平角的定义等知识,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.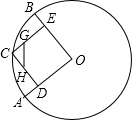 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 不能确定 |
6.已知点A(-4,y1),B(2,y2)都在双曲线y=$\frac{k}{x}$(k>0)上,则y1、y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,连接AE,DB.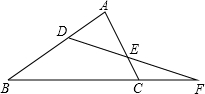 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.
如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.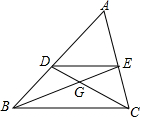 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12. 如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.
如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.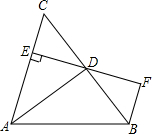 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF. 长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.