题目内容
11.下列各式中,正确的个数是( )①若|$\overrightarrow{a}$|=0,则$\overrightarrow{a}$=0;②若$\overrightarrow{a}$=$\overrightarrow{0}$,则|$\overrightarrow{a}$|=$\overrightarrow{0}$;③若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$-$\overrightarrow{b}$;④若$\overrightarrow{a}$=$\overrightarrow{0}$,则-$\overrightarrow{a}$=$\overrightarrow{0}$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据平面向量与模的定义,求解即可求得答案.
解答 解:①若|$\overrightarrow{a}$|=0,则$\overrightarrow{a}$=$\overrightarrow{0}$;故错误;
②若$\overrightarrow{a}$=$\overrightarrow{0}$,则|$\overrightarrow{a}$|=0;故错误;
③若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,模相等,方向没法确定,故错误;
④若$\overrightarrow{a}$=$\overrightarrow{0}$,则-$\overrightarrow{a}$=$\overrightarrow{0}$,正确.
故选B.
点评 此题考查了平面向量的知识.注意掌握$\overrightarrow{0}$的意义,模的定义是解此题的关键.

练习册系列答案
相关题目
2.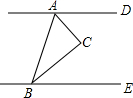 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
5.已知抛物线y=ax2-2ax+m与x轴相交于A(-1,0)、B两点,与y轴负半轴相交于点C,且S△ABC=6,则( )
| A. | 在y轴右侧该抛物线上不存在点M,使S△ACM=3 | |
| B. | 在y轴右侧该抛物线上存在两个点M,使S△ACM=3 | |
| C. | 在y轴右侧该抛物线上存在唯一的点M(2,3),使S△ACM=3 | |
| D. | 在y轴右侧该抛物线上存在唯一的点M(2,-3),使S△ACM=3 |

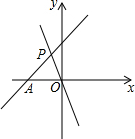 如图,直线y=x+3交x轴于A,与直线y=kx交于点P,且S△AOP=3,求关于x的不等式0<kx<x+3的解集.
如图,直线y=x+3交x轴于A,与直线y=kx交于点P,且S△AOP=3,求关于x的不等式0<kx<x+3的解集.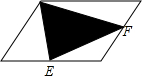 已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积. 已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.
已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.