题目内容
6.关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=2k}\\{2-4y=4k+1}\end{array}\right.$的解满足x>y,求k的范围.分析 代入法求出关于x、y的二元一次方程组,根据x>y得关于k的不等式,解不等式可得.
解答 解:由方程2-4y=4k+1,得:y=$\frac{1-4k}{4}$,
将y=$\frac{1-4k}{4}$代入x+y=2k,得:x+$\frac{1-4k}{4}$=2k,
解得:x=$\frac{12k-1}{4}$,
∵x>y,
∴$\frac{12k-1}{4}>\frac{1-4k}{4}$,
解得:k>$\frac{1}{8}$.
点评 本题主要考查解二元一次方程组、一元一次不等式的能力,解关于x、y的二元一次方程组是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
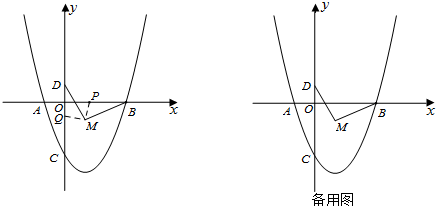
17.如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),交y轴于C点,其部分值对应如下表:
(1)求该二次函数的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.

 点M是AB的中点,∠1=∠2,∠C=∠D,试说明△CAM≌△DBM.
点M是AB的中点,∠1=∠2,∠C=∠D,试说明△CAM≌△DBM.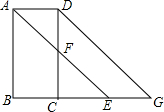 如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB
如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB