题目内容
2.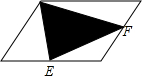 已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
分析 设平行四边形的底和高分别为a和h,再根据阴影部分的面积=平行四边形的面积-三个空白三角形的面积,即可得解.
解答 解:设平行四边形的底和高分别为a和h,
则阴影部分的面积为:ah-$\frac{1}{2}$ah×$\frac{1}{2}$-$\frac{1}{2}$a×$\frac{1}{2}$h×$\frac{1}{2}$-a×$\frac{1}{2}$h×$\frac{1}{2}$
=ah-$\frac{1}{4}$ah-$\frac{1}{8}$ah-$\frac{1}{4}$ah
=ah-$\frac{5}{8}$ah
=$\frac{3}{8}$ah
=128×$\frac{3}{8}$
=48(平方厘米).
答:阴影部分的面积为48平方厘米.
点评 此题主要考查平行四边形和三角形的面积的计算方法的灵活应用.关键是掌握平行四边形的面积为底×高,三角形面积为底×高×$\frac{1}{2}$.

练习册系列答案
相关题目
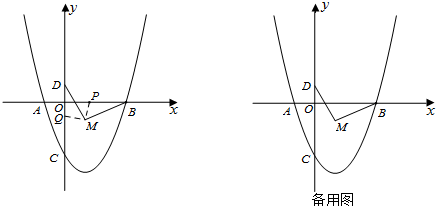
17.如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),交y轴于C点,其部分值对应如下表:
(1)求该二次函数的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.

 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.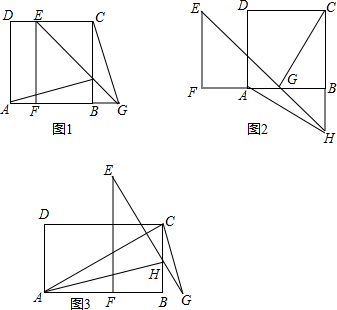
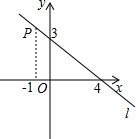 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;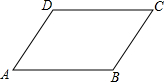 如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.
如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.