题目内容
1.如图1,在平面直角坐标系中有一Rt△AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线l:y=-x2+bx+c经过A、B两点.(1)求抛物线l的解析式及顶点G的坐标.
(2)①求证:抛物线l经过点C.
②分别连接CG,DG,求△GCD的面积.
(3)在第二象限内,抛物线上存在异于点G的一点P,使△PCD与△CDG的面积相等,请直接写出点P的坐标.

分析 (1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式,可求得b、c的值,从而可得到抛物线的解析式,最后依据配方法可求得点G的坐标
(2)由旋转的性质可求得点D和点C的坐标,将点C的横坐标代入抛物线的解析式求得y=0,从而可证明点抛物线l经过点C;如图1所示;过点G作GE⊥y轴,分别求得梯形GEOC、△OCD、△GED的面积,最后依据S△CDG=S梯形GEOC-S△OCD-S△GED求解即可;
(3)如图2所示:过点G作PG∥CD,交抛物线与点P.先求得直线CD的解析式,然后可得到直线PG的一次项系数,然后由点G的坐标可求得PG的解析式,最后将直线PG的解析式与抛物线的解析式联立,最后解得点P的坐标即可.
解答 解:(1)∵OA=1,
∴A(1,0).
又∵tan∠BAO=$\frac{OB}{OA}$=3,
∴OB=3.
∴B(0,3).
将A(1,0)、B(0,3)代入抛物线的解析式得:$\left\{\begin{array}{l}{-{1}^{2}+b+c=0}\\{c=3}\end{array}\right.$,解得:b=-2,c=3.
∴抛物线的解析式为y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点G的坐标为(-1,4).
(2)①证明:由旋转的性质可知;OC=OB=3,
∴C(-3,0).
当x=-3时,y=-(-3)2-2×(-3)+3=-9+6+3=0,
∴点抛物线l经过点C.
②如图1所示;过点G作GE⊥y轴.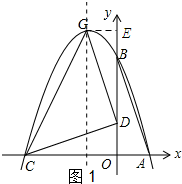
∵GE⊥y轴,G(-1,4),
∴GE=1,OE=4.
∴S梯形GEOC=$\frac{1}{2}$(GE+OC)•OE=$\frac{1}{2}$×(1+3)×4=8.
∵由旋转的性质可知;OD=OA=1,
∴DE=3.
∴S△OCD=$\frac{1}{2}$OC•OD=$\frac{1}{2}$×3×1=$\frac{3}{2}$,S△GED=$\frac{1}{2}$EG•ED=$\frac{1}{2}$×1×3=$\frac{3}{2}$.
∴S△CDG=S梯形GEOC-S△OCD-S△GED=8-$\frac{3}{2}$-$\frac{3}{2}$=5.
(3)如图2所示:过点G作PG∥CD,交抛物线与点P.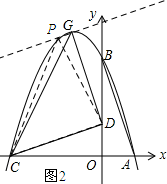
∵PG∥CD,
∴△PCD的面积=△GCD的面积.
∵OD=OA=1,
∴D(0,1).
设直线CD的解析式为y=kx+b.
∵将点C(-3,0)、D(0,1)代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=1}\end{array}\right.$,解得:k=$\frac{1}{3}$,b=1,
∴直线CD的解析式为y=$\frac{1}{3}x$+1.
∵PG∥CD,
∴直线PG的一次项系数为$\frac{1}{3}$.
设PG的解析式为y=$\frac{1}{3}$x+b1.
∵将点G的坐标代入得:$-\frac{1}{3}$+b1=4,解得:b1=$\frac{13}{3}$,
∴直线PG的解析式为y=$\frac{1}{3}x$+$\frac{13}{3}$.
∵将y=$\frac{1}{3}x$+$\frac{13}{3}$与y=-x2-2x+3联立.解得:$\left\{\begin{array}{l}{{x}_{1}=-\frac{4}{3}}\\{{y}_{1}=\frac{35}{9}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=4}\end{array}\right.$,
∴P(-$\frac{4}{3}$,$\frac{35}{9}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、旋转的性质、函数图象上点的坐标与解析式的关系、割补法求不规则图形的面积、以及直线与抛物线的交点问题,求得直线PE的解析式是解题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
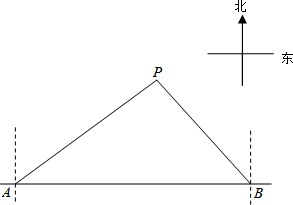 马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4) 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.