题目内容
14.(4y2+4y+1)÷(2y+1)=2y+1.分析 根据完全平方公式先分解因式,再约分得到结果.
解答 解:(4y2+4y+1)÷(2y+1)=(2y+1)2÷(2y+1)=2y+1.
点评 本题考查了分解因式,分式的约分,熟记乘法公式是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
6.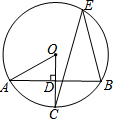 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 6 |
3.如果等腰三角形的两边长分别是方程x2-10x+21=0的两根,那么它的周长为( )
| A. | 17 | B. | 15 | C. | 13 | D. | 13或17 |
4.“黑洞”是恒星演化的最后阶段.根据有关理论,当一颗恒星衰老时,其中心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始坍缩,直到最后形成体积小、密度大的星体.如果这一星体的质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这种收缩使得它的半径达到施瓦氏(Schwarzschild)半径后,其引力就会变得相当强大,以至于光也不能逃脱出来,从而成为一个看不见的星体--黑洞.施瓦氏半径(单位:米)的计算公式是R=$\frac{2GM}{{c}^{2}}$,其中G=6.67×10-11牛•米2/千克2,为万有引力常数;M表示星球的质量(单位:千克);c=3×108米/秒,为光在真空中的速度.已知太阳的质量为2×1030千克,则可计算出太阳的施瓦氏半径为( )
| A. | 2.96×102米 | B. | 2.96×103米 | C. | 2.96×104米 | D. | 2.96×105米 |
 如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.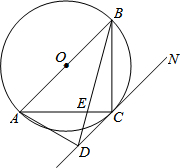 如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.
如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.