题目内容
3．如果等腰三角形的两边长分别是方程x2-10x+21=0的两根，那么它的周长为（ ）| A． | 17 | B． | 15 | C． | 13 | D． | 13或17 |
分析 首先求出方程x2-10x+21=0的两根，然后确定等腰三角形的腰长和底，进而求出它的周长．
解答 解：∵等腰三角形的两边长分别是方程x2-10x+21=0的两根，
∴方程x2-10x+21=0的两个根分别是x1=3，x2=7，
∴等腰三角形的腰长为7，底边长为3，
∴等腰三角形的周长为：7+7+3=17．
故选：A．
点评 本题主要考查了因式分解法解一元二次方程以及三角形三边关系的知识，解答本题的关键是掌握等腰三角形的性质，此题难度一般．
练习册系列答案
相关题目
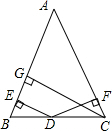如图所示，已知在△ABC中，AB=AC，CG⊥AB，点D是BC边上的一点，DE⊥AB，DF⊥AC．
如图，点A，C，D在同一条直线上，BC与AE交于点F，AE=AC，AD=BC，FA=FC．求证：∠B=∠D．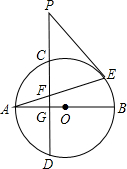
如图，⊙O的直径为AB，弦CD⊥AB于G，PE切⊙O于E交DC延长线于点P，AE交PD于点F．求证：
15．如图，是一个正六棱柱的主视图和左视图，则图中的a=（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2 | D． | 1 |
12．
如图，已知菱形ABCD的对角线AC，BD的长分别为6，8，AE⊥BC，垂足为点E，则AE的长是（ ）
如图，已知菱形ABCD的对角线AC，BD的长分别为6，8，AE⊥BC，垂足为点E，则AE的长是（ ）| A． | $5\sqrt{3}$ | B． | 2$\sqrt{5}$ | C． | $\frac{48}{5}$ | D． | $\frac{24}{5}$ |
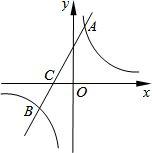如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（-2，0），且tan∠ACO=2．