题目内容
6.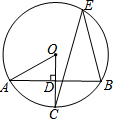 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 6 |
分析 连接OB,由垂径定理可知,AB=2BD,由圆周角定理可得,∠COB=60°,在Rt△DOB中,OD=1,则BD=1×tan60°=$\sqrt{3}$,故AB=2$\sqrt{3}$.
解答 解:连接OB,
∵AB是⊙O的一条弦,OC⊥AB,
∴AD=BD,即AB=2BD,
∵∠CEB=30°,
∴∠COB=60°,
∵OD=1,
∴BD=1×tan60°=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
故选C.
点评 本题主要考查了垂径定理,锐角三角函数及圆周角定理,作出合适的辅助线,运用三角函数是解答此题的关键.

练习册系列答案
相关题目
15.如图,是一个正六棱柱的主视图和左视图,则图中的a=( )


| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 1 |
16.5的绝对值是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | $\frac{1}{5}$ |
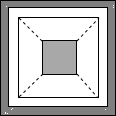 如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π)
如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π) 如图,点A,C,D在同一条直线上,BC与AE交于点F,AE=AC,AD=BC,FA=FC.求证:∠B=∠D.
如图,点A,C,D在同一条直线上,BC与AE交于点F,AE=AC,AD=BC,FA=FC.求证:∠B=∠D.