题目内容
5. 如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为$8\sqrt{3}$,求DF的长.
分析 (1)根据菱形的性质得出CE=CD,CF=CB,再根据矩形的判定证明即可.
(2)根据菱形的面积等于对角线乘积的一半,得出DB的长度,再根据含30°直角三角形的性质解答即可.
解答 (1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)设DB为2a,
∵∠A=60°,菱形ABCD的面积为$8\sqrt{3}$,
∴可得$\frac{1}{2}•2a•2\sqrt{3}a=8\sqrt{3}$,
解得:a=2,
∴DB=4,
∵∠DBC=60°,
∴DF=$4\sqrt{3}$.
点评 此题考查菱形的性质,关键是根据菱形的性质和矩形的判定解答,同时根据菱形的面积和直角三角形的性质分析.

练习册系列答案
相关题目
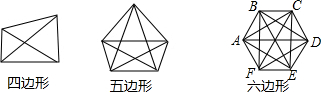
15.连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.观察上述图形并阅读相关文字,思考回答问题:显然四边形对角线有2条;五边形的对角线有5条;对于六边形的对角线条数,光靠“数”数,也能数出来,但已感到较麻烦!需寻找规律!从一个顶点A出发,显然有3条,同理从B出发也3条,每个顶点出发都是3条,但从C顶点出发,就有重复线段!用此方法算出六边形的对角线条数为a;且能归纳出n边形的对角线条数的计算方法;若一个n边形有35条对角线,则a和n的值分别为( )

| A. | 12,20 | B. | 12,15 | C. | 9,10 | D. | 9,12 |
15.如图,是一个正六棱柱的主视图和左视图,则图中的a=( )


| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 1 |
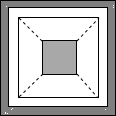 如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π)
如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π)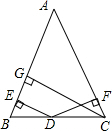 如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.
如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.