题目内容
10.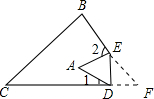 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
分析 根据折叠的性质∠FED=∠AED,∠FDE=∠ADE,根据三角形内角和定理和邻补角的定义即可表示出∠A、∠1、∠2之间的关系.
解答 解:根据题意得∠FED=∠AED,∠FDE=∠ADE,
由三角形内角和定理可得,∠FED+∠EDF=180°-∠F=180°-∠A,
∴∠AEF+∠ADF=2(180°-∠A),
∴∠1+∠2=360°-(∠AEF+∠ADF)=360°-2(180°-∠A)=2∠A.
所以2∠A=∠1+∠2.
故选D.
点评 此题主要考查的是三角形的外角性质和图形的翻折变换,理清图中角与角的关系是解决问题的关键.

练习册系列答案
相关题目
20.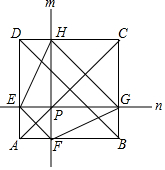 如图,P为边长为4的正方形ABCD的对角线AC上动点(不与A、C重合),过P作直线m、n,分别与AD、AB平行,与正方形各边分别交于E、F、G、H,在以下判断中,不正确的是( )
如图,P为边长为4的正方形ABCD的对角线AC上动点(不与A、C重合),过P作直线m、n,分别与AD、AB平行,与正方形各边分别交于E、F、G、H,在以下判断中,不正确的是( )
 如图,P为边长为4的正方形ABCD的对角线AC上动点(不与A、C重合),过P作直线m、n,分别与AD、AB平行,与正方形各边分别交于E、F、G、H,在以下判断中,不正确的是( )
如图,P为边长为4的正方形ABCD的对角线AC上动点(不与A、C重合),过P作直线m、n,分别与AD、AB平行,与正方形各边分别交于E、F、G、H,在以下判断中,不正确的是( )| A. | P点变化时,四边形EFGH面积保持不变 | |
| B. | P点变化时,六边形DEFBGH面积有最大值12$\sqrt{2}$ | |
| C. | 点P位于正方形ABCD的中心时,DE=2 | |
| D. | P点变化时,六边形DEFBGH周长保持不变 |
5. 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
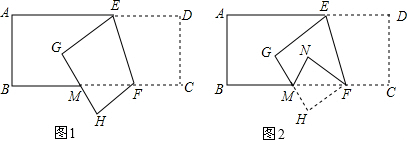
 将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,求CD的长.
将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,求CD的长. 中国古代对勾股定理有深刻的认识.
中国古代对勾股定理有深刻的认识. 如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.
如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.