题目内容
5. 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
分析 过点A作AD∥l1,如图,根据平行线的性质可得∠BAD=∠β.根据平行线的传递性可得AD∥l2,从而得到∠DAC=∠α=40°.再根据等边△ABC可得到∠BAC=60°,就可求出∠DAC,从而解决问题.
解答  解:过点A作AD∥l1,如图,
解:过点A作AD∥l1,如图,
则∠BAD=∠β.
∵l1∥l2,
∴AD∥l2,
∵∠DAC=∠α=40°.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠β=∠BAD=∠BAC-∠DAC=60°-40°=20°.
故选A.
点评 本题主要考查了平行线的性质、平行线的传递性、等边三角形的性质等知识,当然也可延长BA与l2交于点E,运用平行线的性质及三角形外角的性质解决问题.

练习册系列答案
相关题目
10.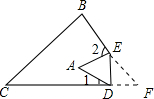 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
15.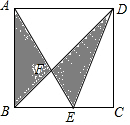 如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
 如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )| A. | $\frac{1}{3}$SABCD | B. | $\frac{1}{6}$SABCD | C. | $\frac{1}{2}$SABCD | D. | $\frac{1}{9}$SABCD |
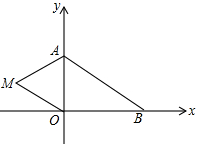 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0. 某人沿坡度为1:3的斜坡从坡底A处行走至坡顶B处,已知AB=3$\sqrt{10}$米,在B处测得AD延长线上一物体C的俯角α为37°,求坡底A到物体C的距离.
某人沿坡度为1:3的斜坡从坡底A处行走至坡顶B处,已知AB=3$\sqrt{10}$米,在B处测得AD延长线上一物体C的俯角α为37°,求坡底A到物体C的距离. 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为64°.
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为64°.