题目内容
20. 如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.
如图所示,在矩形ABCD中,AC,BD相交于点O,H是AD上一动点(H与A,D不重合),且HE⊥AC于点E,HF⊥BD于点F,AG⊥BD于点G,求证:HE+HF=AG.
分析 根据矩形的性质得出OA=OB=OC=OD=$\frac{1}{2}$BD,由三角形面积关系得出OD•AG=AO•HE+OD•HF=OD(HE+HF),即可得出结论.
解答 解:如图,连接OH,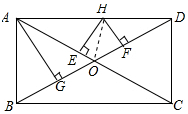
∵四边形ABCD是矩形,
∴OA=OB=OC=OD=$\frac{1}{2}$BD,
∵S△ABD=$\frac{1}{2}$BD•AG,S△AOD=$\frac{1}{2}$AO•HE+$\frac{1}{2}$OD•HF=$\frac{1}{2}$OD•AG,
∴OD•AG=AO•HE+OD•HF=OD(HE+HF),
∴HE+HF=AG.
点评 本题考查了矩形的对角线相等且互相平分的性质,三角形的面积计算;根据三角形的面积求出OD•AG=AO•HE+OD•HF=OD(HE+HF)是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.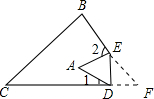 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
8.若∠α与∠β互余.∠α与∠γ互补,则下列中不可能成立的是( )
| A. | α=135°+$\frac{β+γ}{2}$ | B. | γ>β+45° | ||
| C. | ∠β与∠γ有可能互补 | D. | α+β+γ<270° |
15.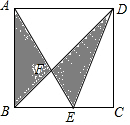 如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
 如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )
如图,正方形ABCD中,E为BC中点,AE、BD交于点F,则阴影部分面积为( )| A. | $\frac{1}{3}$SABCD | B. | $\frac{1}{6}$SABCD | C. | $\frac{1}{2}$SABCD | D. | $\frac{1}{9}$SABCD |
 在△ABC中,AB=AC,E是AB上任意一点,延长AC到F,使BE=CF,连接EF交BC于M.
在△ABC中,AB=AC,E是AB上任意一点,延长AC到F,使BE=CF,连接EF交BC于M.