题目内容
19. 中国古代对勾股定理有深刻的认识.
中国古代对勾股定理有深刻的认识.(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求( a+b)2的值.
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步$\frac{s}{6}$=m;第二步:$\sqrt{m}$=k;第三步:分别用3,4,5乘以k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
分析 (1)根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值,然后根据(a+b)2=a2+2ab+b2即可求解;
(2)先由题中所给的条件找出字母所代表的关系,然后套用公式解题.
解答 (1)解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:$\frac{1}{2}$ab×4=13-1=12,即:2ab=12
则(a+b)2=a2+2ab+b2=13+12=25,即(a+b)2=25.
(2)当S=150时,k=$\sqrt{m}$=$\sqrt{\frac{S}{6}}$=$\sqrt{\frac{150}{6}}$=$\sqrt{25}$=5,
所以三边长分别为:3×5=15,4×5=20,5×5=25,
所以,这个直角三角形的三边长为15,20,25.
点评 本题考查勾股定理,以及完全平方式,正确根据图形的关系求得a2+b2和ab的值是关键.(2)题信息量较大,解答此类题目的关键是要找出所给条件,然后解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.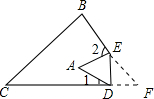 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
8.若∠α与∠β互余.∠α与∠γ互补,则下列中不可能成立的是( )
| A. | α=135°+$\frac{β+γ}{2}$ | B. | γ>β+45° | ||
| C. | ∠β与∠γ有可能互补 | D. | α+β+γ<270° |
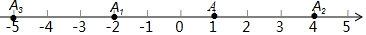 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.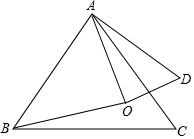 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD, 在△ABC中,AB=AC,E是AB上任意一点,延长AC到F,使BE=CF,连接EF交BC于M.
在△ABC中,AB=AC,E是AB上任意一点,延长AC到F,使BE=CF,连接EF交BC于M.