题目内容
10.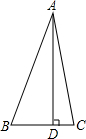 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
分析 将图形分别以AB、AC为对称轴进行翻折变换,易得四边形AEGF是正方形,设AD=x,可得BG=x-2,CG=x-3,在RT△BCG中利用勾股定理可求得x的值.
解答 解:将图形分别以AB、AC为对称轴进行翻折变换如图1.
D点的对称点为E、F,延长EB、FC相交于G点,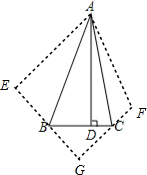
∴∠BAD=∠EAD,∠CAD=∠CAF,AE=AD=AF,
∠E=∠ADB=∠F=∠ADC=90°,
∵∠BAC=∠BAD+∠CAD=45°,
∴∠EAF=90°,
∴四边形AEGF是正方形,
设AD=x,
由题意得,BG=x-2,CG=x-3.
在Rt△BCG中,由勾股定理可得(x-2)2+(x-3)2=52,
解得:x=6
∴AD=6.
点评 本题主要考查翻折变换的应用,通过翻折变换构造一个正方形是此题的难点,熟练掌握翻折变换的性质:(1)对应点所连的线段被对称轴垂直平分,(2)对应线段相等,对应角相等;(3)关于某直线对称的两个图形是全等图形.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
6.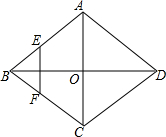 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 7 |
3.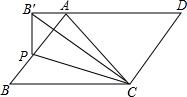 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
5. 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )
 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )| A. | ∠A=∠1+∠2 | B. | ∠A=$\frac{1}{2}$(∠1+∠2) | C. | ∠A=$\frac{1}{3}$(∠1+∠2) | D. | ∠A=$\frac{1}{4}$(∠1+∠2) |
20.若菱形的周长为8,高为$\sqrt{2}$,则菱形两邻角的度数比为( )
| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
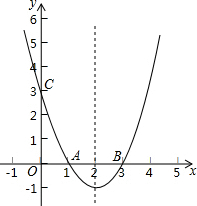 已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.
已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.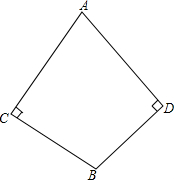 如图,四边形ACBD中,∠C=∠D=90°,BC=BD.求证:AC=AD.
如图,四边形ACBD中,∠C=∠D=90°,BC=BD.求证:AC=AD. 如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.
如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.