题目内容
5.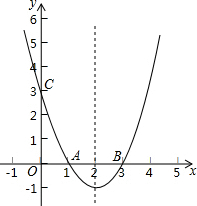 已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.
已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.
分析 连接BC,交抛物线的对称轴于点P,连接PA.先由勾股定理求得AC,BC的长,然后依据轴对称的性质和两点之间线段最短可知PC+AP的最小值为BC,然后将△APC的最小值转为BC+AC求解即可.
解答 解:连接BC,交抛物线的对称轴于点P,连接PA.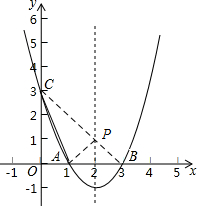
在Rt△COB中,由勾股定理可知:BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=3$\sqrt{2}$,在Rt△COA中,AC=$\sqrt{O{C}^{2}+O{A}^{2}}$=$\sqrt{10}$.
∵点A与点B关于直线x=2,
∴AP=PB.
∴CP+AP=PC+PB.
由两点之间线段最短可知:当点C、P、B在一条直线上时,CP+AP有最小值,
∴CP+AP的最小值=BC=3$\sqrt{2}$.
∴△PAC周长的最小值=AC+BC=$\sqrt{10}$+3$\sqrt{2}$.
点评 本题主要考查的是轴对称路径最短问题,解答本题主要应用了轴对称图形的性质和勾股定理,明确当C、P、B在一条直线上时,CP+AP有最小值时解题的关键.

练习册系列答案
相关题目
 如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.
如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH. 已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长.
已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长. 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长. 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.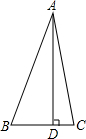 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)