题目内容
5. 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )| A. | ∠A=∠1+∠2 | B. | ∠A=$\frac{1}{2}$(∠1+∠2) | C. | ∠A=$\frac{1}{3}$(∠1+∠2) | D. | ∠A=$\frac{1}{4}$(∠1+∠2) |
分析 由折叠及邻补角的性质可知,∠1=180°-2∠ADE,∠2=180°-2∠AED,两式相加,结合已知可求∠ADE+∠AED的度数,在△ADE中,由内角和定理可求∠A的度数.
解答 解:根据折叠及邻补角的性质,得
∠1=180°-2∠ADE,∠2=180°-2∠AED,
∴∠1+∠2=360°-2(∠ADE+∠AED),
∴∠ADE+∠AED=$\frac{1}{2}$[360°-(∠1+∠2)]=180°-$\frac{1}{2}$(∠1+∠2),
∴在△ADE中,由内角和定理,得
∠A=180°-(∠ADE+∠AED)=180°-180°+$\frac{1}{2}$(∠1+∠2)=$\frac{1}{2}$(∠1+∠2).
故选B.
点评 本题考查了翻折变换,邻补角的性质,三角形内角和定理,关键是把∠1+∠2看作整体,对角的和进行转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.不等式组$\left\{\begin{array}{l}{-x+2<x-4}\\{x>m}\end{array}\right.$的解集是x>3,那么m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m>3 | D. | m<3 |
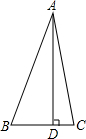 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)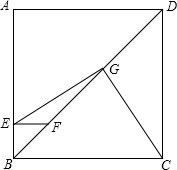 已知正方形ABCD,点F为射线DB上一点,过点F作FE∥AD,FE交射线AB于E,G为FD的中点,连接CG,求证:∠CGE=90°.
已知正方形ABCD,点F为射线DB上一点,过点F作FE∥AD,FE交射线AB于E,G为FD的中点,连接CG,求证:∠CGE=90°.