题目内容
6.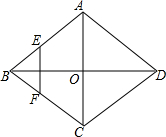 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 7 |
分析 先根据三角形中位线定理求出EF的长,再由菱形的性质求出OA,OB的长,根据勾股定理求出AB的长即可.
解答 解:∵E、F分别是AB、BC边的中点,
∴EF是△ABC的中位线.
∵EF=$\sqrt{3}$,
∴AC=2$\sqrt{3}$.
∵四边形ABCD是菱形,BD=4,
∴AC⊥BD,OA=$\frac{1}{2}$AC=$\sqrt{3}$,OB=$\frac{1}{2}$BD=2,
∴AB=$\sqrt{{OA}^{2}+{OB}^{2}}$=$\sqrt{3+4}$=$\sqrt{7}$.
故选C.
点评 本题考查的是菱形的性质,熟知菱形的对角线互相垂直平分是解答此题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
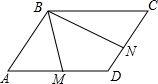 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.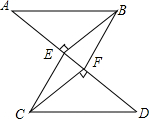 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.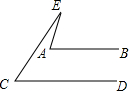 如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.
如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.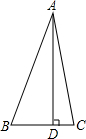 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)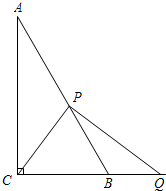 如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.
如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.