题目内容
3.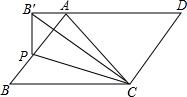 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
分析 由由折叠的性质可得:PB′=PB,∠PB′C=∠B,又由在平行四边形ABCD中,PB′⊥AD,求得△B′CD是直角三角形,继而求得DB′的长,然后设BP=x,在Rt△AB′P中,利用勾股定理即可求得答案.
解答 解:由折叠的性质可得:PB′=PB,∠PB′C=∠B,
∵四边形ABCD是平行四边形,PB′⊥AD,
∴∠B=∠D,∠PB′A=90°,
∴∠D+∠CB′D=90°,
∴∠DCB′=90°,
∵CD=3,BC=4,
∴AD=B′C=BC=4,
∴DB′=$\sqrt{C{D}^{2}+CB{′}^{2}}$=5,
∴AB′=DB′-AD=1,
设BP=x,则PB′=x,PA=3-x,
在Rt△AB′P中,PA2=AB′2+PB′2,
∴x2+12=(3-x)2,
解得:x=$\frac{4}{3}$,
∴BP=$\frac{4}{3}$.
故选A.
点评 此题考查了折叠的性质、平行四边形的性质以及勾股定理.注意掌握折叠前后图形的对应关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.
如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.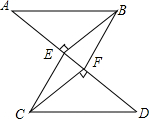 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.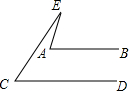 如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.
如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.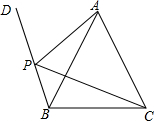 如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.
如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.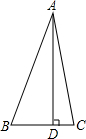 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长(提示:运用轴对称知识,将图形进行翻折变换解答此题)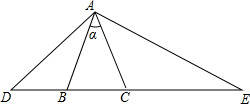 如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数.
如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数.