题目内容
3.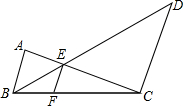 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,(1)求EF的长;
(2)设AB=a,CD=b,求EF的长;
(3)求证:$\frac{1}{{S}_{△ABC}}$+$\frac{1}{{S}_{△DBC}}$=$\frac{1}{{S}_{△EBC}}$.
分析 (1)先由EF∥AB判断△CEF∽△CAB,利用相似三角形的性质得$\frac{EF}{AB}$=$\frac{CF}{CB}$①,再证明△BEF∽△BDC得到$\frac{EF}{CD}$=$\frac{BF}{BC}$②,把两式相加后利用比例的性质即可得到$\frac{1}{EF}$=$\frac{1}{AB}$+$\frac{1}{CD}$,然后把AB和CD的值代入计算即可;
(2)利用(1)的结论易得EF的长;
(3)作AH⊥BC于H,EM⊥BC于M,DN⊥BC于N,如图,与(1)的方法一样可得$\frac{1}{EM}$=$\frac{1}{AH}$+$\frac{1}{DN}$,然后利用等式的性质变形得到$\frac{1}{\frac{1}{2}BC•EM}$=$\frac{1}{\frac{1}{2}BC•AH}$+$\frac{1}{\frac{1}{2}BC•DN}$,从而根据三角形面积公式即可得到结论.
解答 (1)解:∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{EF}{AB}$=$\frac{CF}{CB}$①,
∵EF∥CD,
∴△BEF∽△BDC,
∴$\frac{EF}{CD}$=$\frac{BF}{BC}$②,
①+②得$\frac{EF}{AB}$+$\frac{EF}{CD}$=1,
∴$\frac{1}{EF}$=$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{20}$+$\frac{1}{80}$,
∴EF=16;
(2)解:由(1)得$\frac{1}{EF}$=$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{a}$+$\frac{1}{b}$,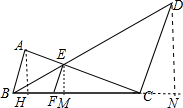 则EF=$\frac{ab}{a+b}$;
则EF=$\frac{ab}{a+b}$;
(3)证明:作AH⊥BC于H,EM⊥BC于M,DN⊥BC于N,如图,
与(1)的方法一样可得$\frac{1}{EM}$=$\frac{1}{AH}$+$\frac{1}{DN}$,
∴$\frac{1}{\frac{1}{2}BC•EM}$=$\frac{1}{\frac{1}{2}BC•AH}$+$\frac{1}{\frac{1}{2}BC•DN}$,
即:$\frac{1}{{S}_{△ABC}}$+$\frac{1}{{S}_{△DBC}}$=$\frac{1}{{S}_{△EBC}}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

| 购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1062 |
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
 如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )
如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )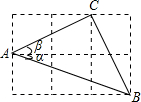 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)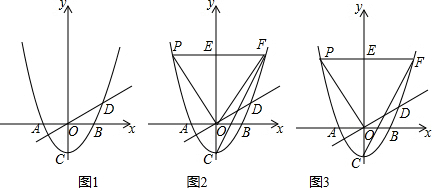
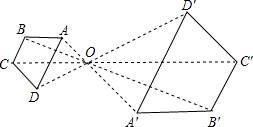 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.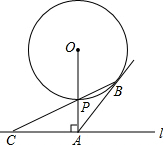 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )
如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )