题目内容
12. 如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )
如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 由勾股定理得出$\sqrt{{5}^{2}+{5}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$,$\sqrt{{7}^{2}+{1}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$,得出不同角度的α有3个即可.
解答 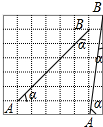 解如图所示:
解如图所示:
∵$\sqrt{{5}^{2}+{5}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$=AB,此时AB与网格线相交所成的锐角α=45°;
$\sqrt{{7}^{2}+{1}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$=AB,此时AB与网格线相交所成的锐角α有两个不同的角度;
∴AB与网格线相交所成的锐角α,不同角度的α有3个;
故选:C.
点评 本题考查了勾股定理、等腰直角三角形的性质;由勾股定理得出$\sqrt{{5}^{2}+{5}^{2}}$=$\sqrt{50}$是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y<505,则a的取值范围( )
| A. | a>2016 | B. | a<2016 | C. | a>505 | D. | a<505 |
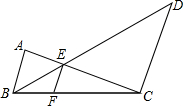 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,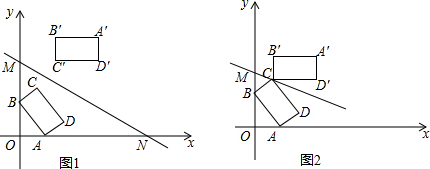
 图中每个小正方形的边长都是1,已知A点可用(3,2)表示
图中每个小正方形的边长都是1,已知A点可用(3,2)表示