题目内容
14.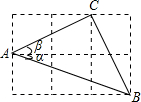 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
分析 根据正切的概念和正方形网格图求出tanα和tanβ,根据等腰直角三角形的性质和tan45°的值求出tan(α+β),比较即可.
解答 解:由正方形网格图可知,tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,
则tanα+tanβ=$\frac{1}{2}$+$\frac{1}{3}$=$\frac{5}{6}$,
∵AC=BC,∠ACB=90°,
∴α+β=45°,
∴tan(α+β)=1,
∴tan(α+β)>tanα+tanβ,
故答案为:>.
点评 本题考查的是特殊角的三角函数值、锐角三角函数的定义以及等腰直角三角形的性质,熟记特殊角的三角函数值、正确理解锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
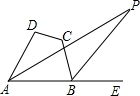 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.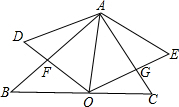 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
 某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.
某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.
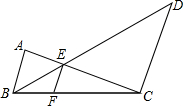 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,