题目内容
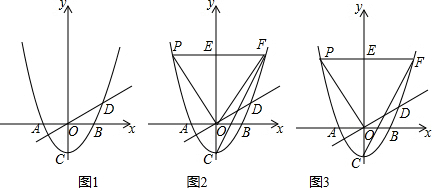
11.如图1,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2+bx+c交x轴于A、B两点,交y轴于点C,OC=3,交直线OD于D,直线OD的解析式为y=$\frac{3}{4}$x,点D的横坐标为4.(1)求此抛物线的解析式;
(2)在(1)中如图2,点P为y轴左侧抛物线上一点,作PE⊥y轴,垂足为E,交抛物线另一侧于F,连接CF,求PE•tan∠ECF的值;
(3)在(2)中如图3,连接OP,M为y轴正半轴上一点,N为射线OD上一点,是否存在点P满足OP=MN,∠PON+∠OMN=180°,且ON=2OM?若存在,求出此时P点的坐标;若不存在,请说明理由.
分析 (1)先求得点C与点D的坐标,然后将点C和点D的坐标代入抛物线的解析式可求得b、c的值,从而得到抛物线的解析式;
(2)设P(t,$\frac{1}{2}$t2-$\frac{1}{2}$t-3),则PE=-t,EC=3=$\frac{1}{2}$t2-$\frac{1}{2}$t,然后依据抛物线的对称性可求得EF=1-t,然后结合锐角函数的定义,将PE、PC、EF的长代入化简即可求得答案;
(3)首先依据题意画出图形,然后MH⊥ON,垂足为H,接下来,证明△OEP≌△NHM,由全等三角形的性质可知MH=PE,OE=NH,设OH=3k,则MH=4k,OM=5k,从而可求得点P的坐标(用含k的式子表示),将点P的坐标代入抛物线的解析式可求得k的值,从而得到点P的坐标.
解答 解:(1)∵OC=3,且点C在y轴的负半轴上,
∴C(0,-3).
将点C(0,-3)代入y=$\frac{1}{2}$x2+bx+c得:c=-3.
∵D点横坐标为4,将x=4代入y=$\frac{3}{4}$x得:y=3,
∴D(4,3).
∵将D(4,3)代入y=$\frac{1}{2}$x2+bx-3得b=-$\frac{1}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{1}{2}$x-3.
(2)设P(t,$\frac{1}{2}$t2-$\frac{1}{2}$t-3),则PE=-t,EC=$\frac{1}{2}$t2-$\frac{1}{2}$t-3+3=$\frac{1}{2}$t2-$\frac{1}{2}$t.
∵抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{1}{2}$,
∴EF=1-t.
∴PE•tan∠ECF=-t•$\frac{1-t}{\frac{1}{2}{t}^{2}-\frac{1}{2}t}$=$\frac{t(t-1)}{\frac{1}{2}t(t-1)}$=2.
(3)如图所示:MH⊥ON,垂足为H.
∵∠OMN+∠PON=180°,∠OMN+∠MON+∠MNO=180°,
∴∠PON=∠MON+∠MNO.
∴∠POM=∠ONM.
在△OEP和△NHM中,$\left\{\begin{array}{l}{∠POM=∠ONM}\\{∠MHN=∠PEO}\\{MN=OP}\end{array}\right.$,
∴△OEP≌△NHM.
∴MH=PE,OE=NH.
∵∠DOB=∠OMH,直线ON的解析式为y=$\frac{3}{4}$x,
∴设OH=3k,则MH=PE=4k,OM=5k.
∵ON=2OM,
∴ON=10k,HN=7k.
∴OE=7k.
∴P(-4k,7k).
将点P(-4k,7k)代入y=$\frac{1}{2}$x2-$\frac{1}{2}$x-3得:$\frac{1}{2}$×(-4k)2-$\frac{1}{2}×$(-4k)-3=7k,解得:k=1,k=-$\frac{3}{8}$(舍去).
∴P(-4,7).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、抛物线的对称性、全等三角形的性质和判定、勾股定理的应用,一次函数的图象和性质,用含k的式子表示点P的坐标是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | a>2016 | B. | a<2016 | C. | a>505 | D. | a<505 |
 如图,一人乘雪橇沿斜坡下滑AB=72米,且∠A=28°,则他下降的铅直高度BC为33.8米.(用科学计算器计算,结果精确到0.1)
如图,一人乘雪橇沿斜坡下滑AB=72米,且∠A=28°,则他下降的铅直高度BC为33.8米.(用科学计算器计算,结果精确到0.1) 某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.
某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.
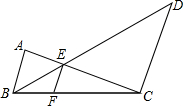 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,