题目内容
8.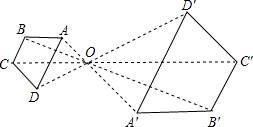 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.
分析 由以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,可求得四边形ABCD和四边形A′B′C′D′的位似比,继而求得四边形ABCD和四边形A′B′C′D′的周长的比.
解答 解:∵以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,OA=4,OA′=8,
∴四边形ABCD和四边形A′B′C′D′的位似比为:OA:OA′=4:8=1:2,
∴四边形ABCD和四边形A′B′C′D′的周长的比为:1:2.
故答案为:1:2..
点评 此题考查了位似变换与相似多边形的性质.注意位似就是相似,相似三角形的周长的比等于相似比.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y<505,则a的取值范围( )
| A. | a>2016 | B. | a<2016 | C. | a>505 | D. | a<505 |
18.平面直角坐标系中,点(-2,4)关于x轴的对称点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,AB是半⊙O的直径,点C在半⊙O上,∠B=∠DCA,AD∥BC,连结OD、AC.
如图,AB是半⊙O的直径,点C在半⊙O上,∠B=∠DCA,AD∥BC,连结OD、AC. 某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.
某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图(不完整),则图中m的值是0.05.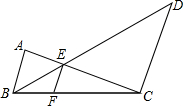 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,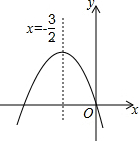 如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.