题目内容
15.已知点A(-3,-4)和B(-2,1),试在y轴求一点P,使PA与PB的和最小.分析 求出A点关于y轴的对称点C,连接BC,交y轴于点P,则P即为所求点,用待定系数法求出过BC两点的直线解析式,求出此解析式与y轴的交点坐标即可.
解答 解:A关于y轴的对称点是C(3,-4)则PA=PC,B,C在y轴两侧 则当BPC共线时,PB+PC最小,即PA+PB最小,
设直线BC是y=kx+b,把B,C两点坐标代入:
$\left\{\begin{array}{l}{1=-2k+b}\\{-4=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$
所以y=-x-1
y轴上x=0,则y=0-1=-1,
所以 P(0,-1).
点评 本题考查的是最短线路问题及用待定系数法求一次函数的解析式,熟知轴对称的性质及一次函数的相关知识是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)前5个正方形分割的三角形的和40前n个正方形分割的三角形的和n2+3n,
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
7.已知一组正数a,b,c,d的平均数为2,则a+2,b+2,c+2,d+2的平均数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
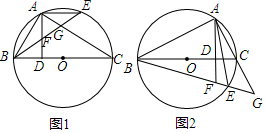
5.已知AB是圆O的直径,点C,P在圆O上,PB=2$\sqrt{3}$,∠ABP=30°,PC=BC,则△PBC的面积为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$或3$\sqrt{3}$ | D. | $\sqrt{3}$或4$\sqrt{3}$ |
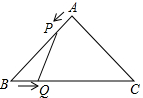 如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.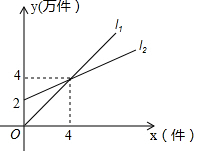 如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)
如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)