题目内容
13.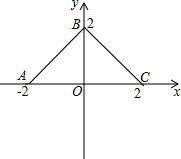 如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.
如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.(1)求S关于t的函数S=f(t)的解析式;
(2)求:当t为何值时,面积S有最大值,最大值是多少?
分析 (1)根据待定系数法,可得AB,BC的解析式,根据自变量与函数值的对应关系,可得M,N,根据三角形的面积,可得函数关系式;
(2)根据二次很熟的性质,可得答案.
解答 解:(1)如图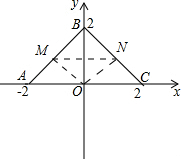 ,
,
由A(-2,0),B(0,2),得
AB的解析式为y=x+2,
当y=t时,x+2=t,解得x=t-2,即M(t-2,t);
由C(2,0),B(0,2),得
BC的解析式为y=-x+2,
当y=t时,-x+2=t,解得x=2-t,即N(2-t,t).
MN=2-t-(t-2)=4-2t,
S=$\frac{1}{2}$MN•yM=$\frac{1}{2}$(4-2t)•t=-t2+2t,
(2)S═-t2+2t=-(t-1)2+1,
当t=1时,S最大=1,
当t=1时,面积S有最大值,最大值是1.
点评 本题考查了二次函数的应用,利用三角形的面积得出二次函数是解题关键.

练习册系列答案
相关题目
8.若x=1是一元二次方程x2+2x+m=0的一个根,则m的值为( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
3.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)前5个正方形分割的三角形的和40前n个正方形分割的三角形的和n2+3n,
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
 如图,已知等腰直角△ABC的直角边长与正方形DEFG的边长均为8cm,EF与AC在同一条直线上,开始时点A与点F重合,让△ABC向左移动,运动速度为1cm/s,最后点A与点E重合.
如图,已知等腰直角△ABC的直角边长与正方形DEFG的边长均为8cm,EF与AC在同一条直线上,开始时点A与点F重合,让△ABC向左移动,运动速度为1cm/s,最后点A与点E重合.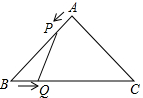 如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.